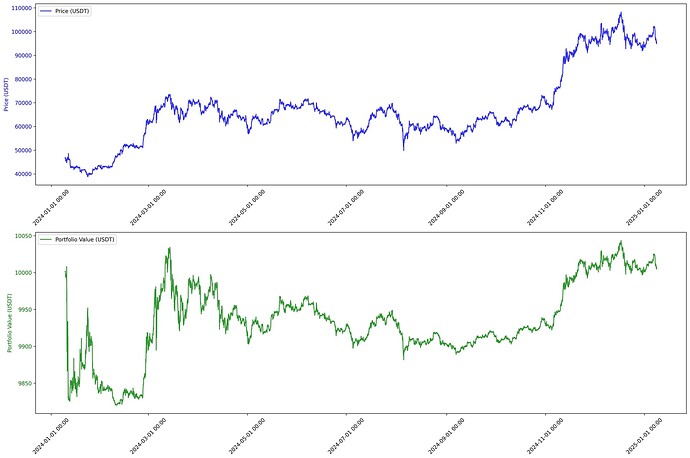
DeworkHub|基于凯利公式的 BTC/USDT 量化交易策略
凯利公式(Kelly Criterion)是由约翰·凯利(John Kelly)在 1956 年提出的一种资金管理方法,旨在最大化长期资金增长率。其核心思想是根据胜率和赔率动态调整每次投资的仓位。
凯利公式的数学表达式为:
f^{*}=\frac{bp-q}{b}
其中:
-
f^{*} :最优投资比例(仓位比例)
-
b :赔率(盈利金额与亏损金额的比值)
-
p :胜率(盈利概率)
-
q :败率(亏损概率), q=1-p
废话不多说,上代码:
import ccxt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from datetime import datetime, timedelta
# 初始化 OKX 交易所
exchange = ccxt.okx()
# 设置参数
symbol = 'BTC/USDT' # 交易对
initial_balance = 10000 # 初始资金 10,000 USDT
taker_fee = 0.0006 # 吃单费率 0.06%
maker_fee = 0.0002 # 挂单费率 0.02%
slippage = 0.0005 # 滑点 0.05%
stop_loss = 0.05 # 止损比例 5%
take_profit = 0.10 # 止盈比例 10%
# 获取过去一整年的 1 小时线数据
def fetch_ohlcv(symbol, timeframe='1h', days=365):
since = exchange.parse8601((datetime.utcnow() - timedelta(days=days)).strftime('%Y-%m-%d %H:%M:%S'))
ohlcv = []
while True:
data = exchange.fetch_ohlcv(symbol, timeframe=timeframe, since=since)
if not data:
break
since = data[-1][0] + 1 # 下一批数据的起始时间
ohlcv.extend(data)
if len(data) < 100: # 如果数据不足 100 条,说明已经获取完所有数据
break
df = pd.DataFrame(ohlcv, columns=['timestamp', 'open', 'high', 'low', 'close', 'volume'])
df['timestamp'] = pd.to_datetime(df['timestamp'], unit='ms')
return df
# 计算收益率
def calculate_returns(df):
df['return'] = df['close'].pct_change()
return df
# 计算胜率和赔率
def calculate_kelly_params(df):
wins = df[df['return'] > 0]['return']
losses = df[df['return'] < 0]['return']
p = len(wins) / len(df) # 胜率
b = wins.mean() / abs(losses.mean()) # 赔率
return p, b
# 凯利公式计算最优仓位
def kelly_criterion(p, b):
return (b * p - (1 - p)) / b
# 策略逻辑
def run_strategy(symbol):
df = fetch_ohlcv(symbol, timeframe='1h', days=365) # 获取过去一整年的 1 小时线数据
df = calculate_returns(df)
p, b = calculate_kelly_params(df)
f_star = kelly_criterion(p, b) # 最优仓位比例
balance = initial_balance
asset_values = [] # 存储资产价值
positions = [] # 存储仓位状态
for i in range(1, len(df)):
current_price = df['close'].iloc[i]
return_rate = df['return'].iloc[i]
# 动态调整仓位
if i % 24 == 0: # 每天重新计算一次仓位
p, b = calculate_kelly_params(df.iloc[:i])
f_star = kelly_criterion(p, b)
# 计算仓位
position_size = balance * f_star # 根据凯利公式计算仓位
# 模拟交易
if return_rate > 0: # 盈利
pnl = position_size * return_rate * (1 - taker_fee - slippage)
else: # 亏损
pnl = position_size * return_rate * (1 - taker_fee - slippage)
# 止损和止盈
if pnl < -balance * stop_loss:
pnl = -balance * stop_loss
elif pnl > balance * take_profit:
pnl = balance * take_profit
# 更新资金
balance += pnl
asset_values.append(balance)
# 创建图表
plt.figure(figsize=(18, 12))
# 子图 1: 价格走势
ax1 = plt.subplot(2, 1, 1)
ax1.plot(df['timestamp'], df['close'], label='Price (USDT)', color='blue', alpha=0.8)
ax1.set_ylabel('Price (USDT)', color='blue')
ax1.tick_params(axis='y', labelcolor='blue')
ax1.legend(loc='upper left')
# 子图 2: 资产价值
ax2 = plt.subplot(2, 1, 2)
ax2.plot(df['timestamp'][1:], asset_values, label='Portfolio Value (USDT)', color='green', alpha=0.8)
ax2.set_ylabel('Portfolio Value (USDT)', color='green')
ax2.tick_params(axis='y', labelcolor='green')
ax2.legend(loc='upper left')
# 格式化日期
for ax in [ax1, ax2]:
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d %H:%M'))
plt.setp(ax.xaxis.get_majorticklabels(), rotation=45)
# 保存高分辨率图片
plt.tight_layout()
plt.savefig(f'{symbol.replace("/", "_")}_kelly_strategy.jpg', dpi=300, bbox_inches='tight')
print(f"Chart saved as {symbol.replace('/', '_')}_kelly_strategy.jpg")
plt.show()
# 运行策略
run_strategy(symbol)
可见凯利公式在投资过程中,稳中求进,是一种获取长期稳定回报的不错选择。