Article Source :https://medium.com/platon-network/techsharing/home
The development of the consensus mechanism from PoW to PoS is in face of a common problem — “who generates the blocks” and how to maintain the network operation securely and efficiently. We will use two articles to analyze in detail the challenges faced, as well as the existing solutions in the industry and the PlatON’s solution.
Blockchain technology, as being decentralized, immutable, verifiable, and traceable, has been attached great significance by governments, financial institutions, and social organizations, etc. As the core of blockchain, the “consensus mechanism” determines the important properties of blockchain such as security, decentralization, and scalability, therefore, is particularly important.
The PoW consensus mechanism, which was initially proposed by Bitcoin, keeps calculating the solution to a problem with computing power to obtain the right to bookkeeping, causing waste of resources and inefficiency. What’s more, the computing-power monopoly of major mining pools also undermines decentralization.
The PoS consensus mechanism of the Staking Economy was then proposed, which associates bookkeeping rights with the staking owned, and the percentage of staking is proportional to the probability of acquiring bookkeeping rights. In this mechanism, the producer nodes and the validators are selected by staking, the blocks are proposed by the producer nodes, and a group of validators perform consensus on the blocks to solve the problems of resource waste and inefficiency in the PoW mechanism.
Random number scheme
Essentially, PoW and PoS are both addressing the problem of selecting the person to generate blocks and how to reach consensus on the blocks securely and efficiently to maintain a distributed ledger.
For better decentralization and security, the selected nodes need to be random. Hence, the key problem is to obtain a safe and consistent random number that everyone agrees on.
If the data within the block is directly used to generate random numbers, then the block generation node can control the generation of random numbers by adjusting the data within the block, and they would obtain the bookkeeping rights preemptively, thus manipulating the chain. This would raise security issues, so major cryptography-based schemes were born.
VRF
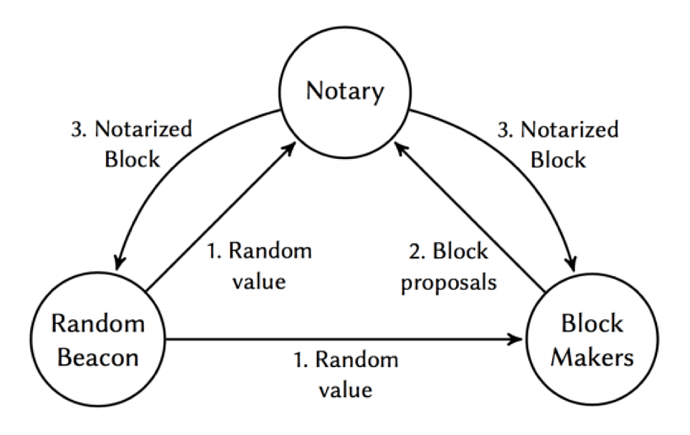
Currently, many teams are using VRF (Verifiable Random Functions) to generate random numbers for the selection of block producers and validators. Each node uses random numbers and staking (account balance) in private to secretly draw lots, and calculates whether a certain threshold is reached (whether it is a producer or validator), and then the node identity and block are publicized at the same time, so that the nodes are protected from attacks disrupting them from producing blocks, and therefore has a higher level of security. The overall scheme is posteriori (announce the block first and verify the identity later), but requires multiple steps to reach consensus on the block due to its secret lottery and changing of validators with each round of voting.
BLS Threshold Signature
The BLS Threshold Signature is also used to generate random numbers through which the producer and verification group of the blocks are selected to reach consensus. Randomness created with the threshold mechanism solves the critical “last participant” problem, where the last participant in the protocol knows the next random value and can decide to abort the protocol. However, since the members of each group are pre-determined, it is not posteriori and is deficient in security, in addition, a large number of members of the groups means the volume of communication is huge, and they have to ensure that most nodes are online, which is inefficient.
PVSS
The selection of validators is based on the proportion of staking and probability to select the block producers. While the random number is generated collaboratively by using PVSS (Publicly Verifiable Secret Sharing), which ensures the result generated is unpredictable and will not be aborted. The nodes are selected based on staking with the FTS (Follow-The-Satoshi) algorithm, rendering the whole selection process random and decentralized. The PVSS, which can be proved to be secure and robust, is the first PoS algorithm that is raised by the academic community and adopted by the industry.
VDF
Proposed by cryptography professor of Stanford Dan Boneh and his colleagues in their paper Verifiable Delay Function, VDF is a mathematical function that guarantees the uniqueness of the result and the seriality of the process. The function accepts some input parameters (data, time, etc.) and guarantees that the computation takes at least a certain amount of time before the result is obtained, and the validators can quickly verify the correctness of the result based on the input parameters.
The features of VDF can be applied to enhance security, for example, when multiple parties interact to generate data or get data from a certain source, instead of applying the results directly, the results are entered into VDF to avoid prediction and manipulation of the results.
Summary
Various implementation schemes propose different solutions from different perspectives, and they each have their own merits. But no matter how the various types of randomized selection schemes are implemented, they should all put decentralization, security, and high performance as the ultimate goal.
The design objectives and implementation of PlatON
PlatON adopts the PPoS consensus mechanism to produce and sign blocks with a set of validators, providing guaranteed operation that is secure and efficient. The operation of the entire network is highly decentralized, and every stake-owner in the network can become a member of it, participating in the maintenance of the entire network and earn rewards from it. A node can stake a certain amount of LAT to meet the threshold to run for a validator (LAT represents staking). The probability of a node becoming a validator is proportional to the staking it has, and the holders of LAT can delegate their LAT to a node for voting. Thus, if a malicious node commits evil, then a portion of its staked LAT will be forfeited, making the attack more costly and resistant to Sybil Attacks (multiple identities attacks) and Nothing At Stake Problems.
The key is to make sure that the selection of validators is related to the node staking and ensures randomness, making the selection result unpredictable, non-manipulable, fair, and reliable. We divide it into two parts, “random number generation and validator selection”.
Random number generation
A random number used to implement a random selection of validators needs to possess the following properties:
Unpredictability: unable to infer subsequent results from past sequences
Collision-Resistance: different inputs generate different results
Certainty: the results generated from a given input are identical
Randomness: the data sequence is haphazard
Verifiability: the legitimacy of results can be verified
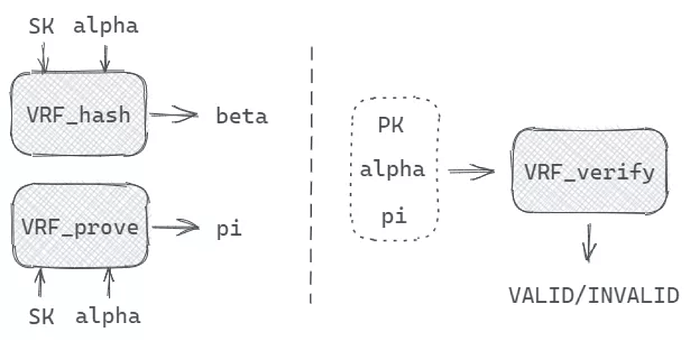
PlatON generates random numbers based on VRF (Verifiable Random Function) since it is unpredictable, collision-resistant, and verifiable, here’s how:
The VRF_hash and VRF_prove function output a hash value and proof by inputting SK (private key) and alpha (seed). The proof is used to verify the correctness of the Hash value of the random number, and the validators can check the legitimacy of the random number by using the public key, the seed, and the proof.
The random number generated based on VRF has these basic properties:
High efficiency: no network communication and fast local generation
Uniqueness: the output is fixed for fixed secret keys and inputs
Collision-Resistance: it is computationally infeasible to obtain the same output from different inputs
In the operation of PlatON, the producer of each block will generate a random number while producing the block, and the random number is generated with the node private key and the random number of the previous block. Honest nodes will complete the production sequentially, and malicious nodes will not be able to manipulate the output of the results. If they conceal the results and do not publish them, malicious nodes will be severely punished.
Selection of block producer
With the above steps, a reliable random number is generated, and if it is directly used to select the validator from the nodes, no additional LAT is needed for the nodes to stake, and this will contribute to:
Security: on the one hand, too many LATs in circulation will introduce attack and stability risks, and on the other hand, a node can increase the probability of being selected as a validator by splitting the LAT owned by itself and staking them into multiple nodes.
Fairness: each node will stake the same amount of LAT because staking more LAT will not bring any change to the node.
Therefore, the probability of being selected should be proportional to the amount of LAT, and splitting the LAT cannot give you a higher probability of being selected.
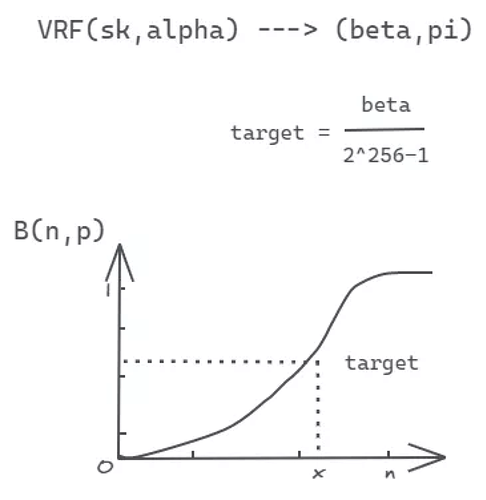
According to the cumulative distribution function properties, the probability distribution of a real random variable X can be completely described.
PlatON uses the binomial distribution cumulative distribution function B(n,p) for random pick, with n representing the total staking of the nodes, and p representing the expected probability.
Each node is randomly selected by this probability mechanism, which is transparent, reversible and, non-manipulable. At this point, the selection of the validator by the probability distribution function is completed.
Summary
In the mechanism, the random numbers are generated locally and efficiently by VRF without interaction. Then, the selection is conducted securely and fairly with the binomial distribution. Next, each validator completes consensus efficiently within the group through the Giskard algorithm to better balance scalability, security, and decentralization.
PlatON is always designed to enhance the degree of decentralization, security, and scalability, striving to reach optimal status on the impossible triangle.