本文系以太坊基金会研究员Dankrad Feist和PlatON算法科学家谢翔博士联合撰写,主要剖析以太坊2.0在可拓展性、数据可用性、托管策略、MPC等方面的探索实现。目前PlatON已发起一个由以太坊基金会资助的项目,实现和优化托管证明的MPC协议,并在GitHub上开源。
1. 以太坊2.0
以太坊是当前世界上使用最为广泛的区块链系统之一。经过约五年的发展,目前已进入第四个阶段——『宁静』(Serenity),也就是广为所知的以太坊2.0,通常简称为ETH 2.0。
以太坊2.0 将会成为迄今为止最具雄心的一次升级,其设计目的涉及到改善去中心化系统的各个方面。一旦升级成功,目前以太坊网络的两大难题将会被解决,它们分别是 可扩展性和可持续性 。
1.1. 可扩展性
当前以太坊网络的能力大约为20 TPS,这远无法满足成百上千个应用程序的使用需求。 以太坊社区提出了许多解决扩展性的方案,Eth 2.0最终决定采用分片的方式来实现Layer 1 层的扩展 。
简而言之,通过分片的方式可将系统分为可管理的较小部分(分片链),并且每一分片各自独立并行处理。最后,每个分片的结果将通过交联(crosslink)到信标链连接在一起。
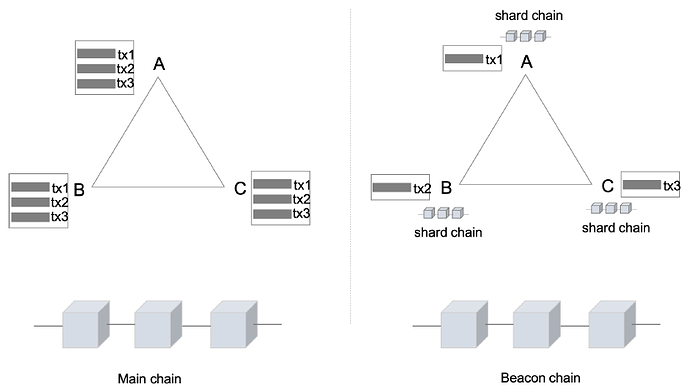
举一个简单的例子,假设一个区块包含三笔交易。在当前的以太坊网络中,每个节点(例如节点A、B、C)必须验证所有交易。若算力最差的节点需3 秒来验证该块,则系统的吞吐量为1TPS。显然,系统的可扩展性取决于单个节点的处理能力。
在分片中,交易可被分配给不同的分片链,每一个节点仅需验证其中一个分片即可。交易也被分成三部分,每一部分在单独的分片中分别进行验证。假设每笔交易可以在1 秒内完成验证,那么整个系统的吞吐量将变为3TPS!此外,每个节点不需要存储链中的所有数据,它们仅需负责在某些时期对于一些特定分片数据的存储。
当然,在实际情况中,每一分片可被多个验证人节点验证。若对此感兴趣,可进一步参考Sharding FAQ【1】。ETH 2.0 目标是打造1024 个分片(现阶段开启64 个),其吞吐量相比当前网络预期将提高1000 倍。加上layer 2 层的扩展机制,其性能将会进一步提高。
1.2. Proof of Stake
当前的以太坊和比特币一样,依赖于工作量证明(PoW)来保证系统的共识。在PoW系统中,“矿工”通过消耗电力资源来解决密码学难题,并且会因为解决难题而获得奖励。安全性源于计算问题的难度,由于“挖矿”所存在的巨额收益,因此造成一些矿池的中心化和垄断,使得系统的安全性大大折扣。
不仅仅是中心化,挖矿/工作量证明还存在许多其它的问题。譬如,由于计算所消耗的电力资源引起的极大浪费,而消耗能源本身是用来保证系统安全性的,所以这在PoW范式中很难解决。另外,系统只有奖励机制,却不会因为恶意行为而受到惩罚。因此实际上,安全性的开销要比所需的远高的多。
为了解决这些问题,以太坊2.0 将会切换到Proof of Stake(PoS),该协议称为Casper。在PoS系统中,“挖矿”过程替换为一个投票系统,验证人节点需要质押32 个以太币才能参与系统并进行投票。为了达成共识,验证人节点轮流对下一个区块进行提议和投票。如Ethereum Proof of Stake FAQ【2】所述。
此区块链系统维护一组验证人节点列表,任何持有其基础密码货币(以太坊中为以太币)的用户,都可通过发送特定类型的交易进行“锁仓”来成为验证人节点。生成并就新区块达成一致的的过程通过共识算法来完成,共识过程所有节点都可参与。
信标链将成为以太坊2.0 的核心,它存储并维护所有验证人节点的注册,处理跨分片通讯以及最终一致性的确认。 所有的分片始终遵循信标链,持有32 个ETH(固定值)的用户可成为验证人节点。在一个周期中的每一时段,系统从信标链中随机选择委员会指派给不同的分片。验证人节点最终被划分为多个不同的委员会,每个委员会至少由128 位验证人节点组成。该委员会负责在特定的分片上生成区块。
另一方面,验证人节点也会因出现不良行为或不诚实行为而受到惩罚,最严重的的一种惩罚(Slashing),将会销毁节点所有质押的以太币。其他一些情节轻微的惩罚行为包括:不在规定时间正常运行,证明尚未最终确定的区块等。对于双签或者对错误的计算进行签名都会施以最严厉的处罚。
2. 数据可用性问题
数据可用性问题与欺诈证明高度相关,简要说明如下。更多详细信息请参见这篇【3】。
2.1. 欺诈证明
在上面对区块链中的节点(不考虑分片)的描述中,我们实际上指的是全节点。全节点产生链的区块,下载每个节点中的所有数据,并验证所有交易和状态的有效性。一个全节点要求机器配置大量的内存,强大的计算能力以及非常高的带宽。而像手机这样的受限设备很难满足这样的配置要求。
轻节点或者轻客户端是全节点的一种低成本替代方案。它们至少连接到一个全节点上,并且仅下载区块头和想要的区块数据。他们信任全节点来检查数据的有效性,并假定恶意全节点无法创建一条有效的分叉链。
欺诈证明 是针对轻节点的一种机制,它用于降低被非法链欺骗的安全风险。每当诚实的全节点发现某种不一致的状态时,全节点就会生成一个欺诈证明,并为轻节点发出“警报”。此欺诈证明很小,并且可快速在网络进行分发,而且可以肯定地证明某些链的确存在故障。这样,轻节点就可以完全忽略此非法的链,并避免其可能导致的系统状态不一致。
例如,若全节点发现一笔交易t是错误的,此交易的前后状态分别为S_in和S_out。那么全节点构造出此笔交易对应的欺诈证明为(S_in, t, S_out)以及相应的Merkle根(Merkle root)。证明本身非常小,很容易广播以及验证。轻节点可通过验证Merkle根和交易三元组确定交易的非法性。
数据可用性问题 指的是,若某些恶意的全节点对区块头进行了签名,但却不发布区块中的某些数据,该怎么办?特别是如果数据里包含了一笔非法交易(例如,一笔窃取转账金额,并转移至另一账户的交易)该如何?在这种情况下,诚实的全节点无法生成欺诈证明,这是由于缺乏生成欺诈证明所必需要的数据。
2.2. 分片中的数据可用性
数据可用性问题在分片中也尤其重要。 如前所述,ETH 2.0 中的验证人节点不会验证所有区块,也不会去下载所有数据。这是为了让分片机制充分发挥效用,并减轻单个验证人节点的负担。分片区块将由委员会验证,并且只有承诺值会存储在信标链中。从这个角度来看,验证人除了需要一直持续性的参与网络获得之外,它们实际上可看做是大多数分片上的轻节点。
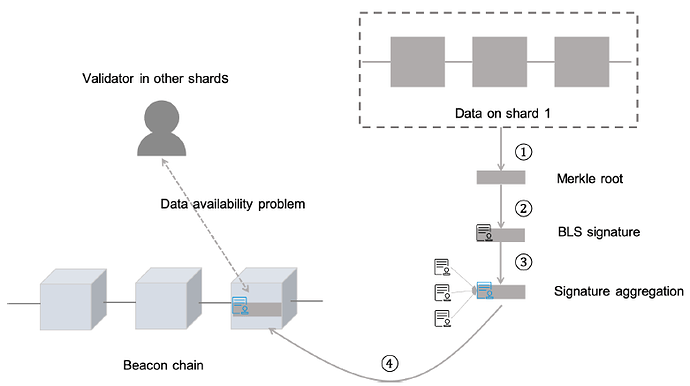
分片中的数据可用性问题描述如下图所示:
整体过程可用以下步骤说明:
分片数据以Merkle 结构存储得到Merkle根。事实上这是交联(crosslink)数据根,为简便起见,将其称为Merkle 根。
提议人节点生产新区块并对Merkle根进行签名;
其他验证人节点对此区块进行投票并签名。其中,BLS签名可聚合成一个签名;
当签名的数量超出门限时,签名的Merkle根就会被添加到信标链上。
在其它分片上发挥作用的分片无法获知完整的区块链数据,并且也不会去下载,否则,这会直接消除分片所带来的优势。这种情况下的数据可用性问题指的是,如何能够验证分片1 中的数据确实可被任何想要下载或验证此数据的全节点所获取。
3. 托管策略(Custody Game)
Eth 2.0 假定2/3的验证人节点是诚实的,并且以这样一种方式将验证人节点分配给对应的分片 :若满足2/3的验证节点诚实,则永远不会将不可用或者不正确的区块包含在一个交联中。但是,这里的“诚实”意味着什么呢?可能有一些验证人节点“诚实但懒惰”:鉴于在大多数情况下,没有人试图作弊,因此节点可能永远都需要真正验证任何内容,而只是对任何传入的区块头进行签名。或者,为了更加安全一些,可先等待该区块头积攒了一些签名之后,然后再继续签名。这种方式仍然可以获得奖励,但却几乎不需要做任何工作。
如果发生这种情况,攻击者可以依靠这些验证人节点促进无效区块的传播。这对于系统的整体运行状况将会带来灾难性的影响。因此,我们希望尽可能避免使用“诚实但懒惰”的验证人节点,这也正是采用Custody Game的目的。
Custody Game本身不能完全解决数据可用性问题。因此,需要额外进行数据可用性检查。但是,它可以确保至少在分片1 中对此区块进行签名的验证人节点都拥有数据。
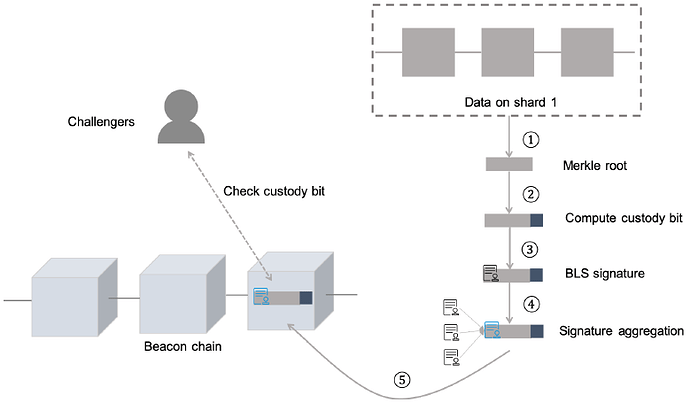
粗略来说,在Custody Game中,每一个验证人节点必须计算出另外的一个托管比特(custody bit)。此托管比特仅可由持有“秘密”密钥(托管密钥,custody key)和数据的验证人节点计算出来。在公布托管密钥后,任何人都可使用数据来验证这一托管比特。若发现一个无效的托管比特,可在链上对此进行挑战。如果挑战者是正确的,那么他们将得到奖励,并且托管比特生成方将会被处罚。
托管证明(proof of custody)存在以下几个关键点:
托管密钥是从验证人节点密钥中确定性地计算出来,以避免采用新的密钥增加系统复杂性。托管密钥会周期性地生成,并且在托管周期结束时公布出来。任何人都可验证托管密钥的有效性。它也被称为临时密钥(ephermeral key),因为它仅在一个托管周期阶段有效(Eth 2.0 中,托管周期大约为9 天)。
若没有托管密钥和数据,那么生成托管比特的方式与随机猜测并无太大区别。
任何人都可以使用托管密钥和数据来检验托管比特的有效性。
在Eth 2.0 中,验证人节点的公钥将是BLS签名系统的公钥。一旦质押以太币成为验证人节点,对应的运营者将生成一个公私钥对。对于每一个托管周期(9 天),验证人节点都能够生成临时托管密钥ek。临时密钥实际上是对计数器(当前周期的计数)的BLS签名。由于BLS的签名过程是确定性的,因此所有的临时密钥都可预先由公钥完全决定。除了验证人节点本身之外,任何人都无法计算出临时密钥。
托管比特是通过某一类mix函数计算而来,尽管函数的具体形式仍在讨论中,但其规范倾向于使用MPC友好的构造,详见eth2.0-specs【4】。总的来说,托管比特的生成方式为b=mix(ek,D),其中D为区块数据。
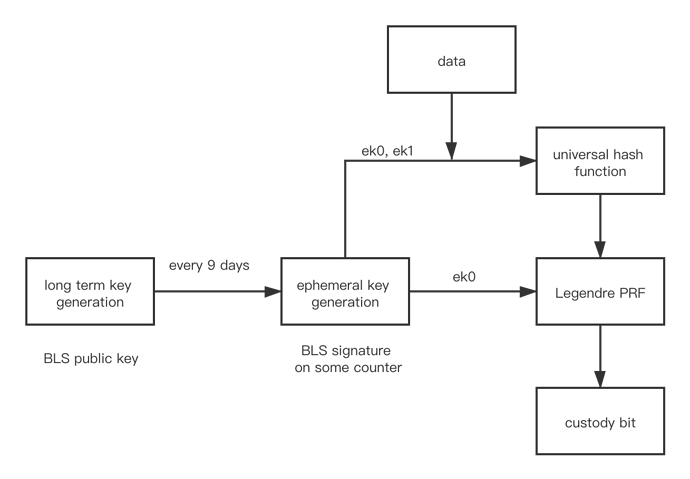
目前,mix函数的构造使用了通用哈希函数(Universal Hash Function,UHF)和勒让德伪随机函数(Legendre PRF)。这些函数均为带密钥的函数并且是确定性的。因此,给定一个密钥ek,将其表示成两个元素ek0, ek1。然后,验证人节点可计算出托管比特b= Leg_PRF(ek0, UHF(ek0,ek1,D)),如下图中的流程所示:
简而言之,UHF用于扩展输入数据空间(密码学中的常用的技术),同时避免外包计算(只有密钥和数据所有者才能计算UHF 函数)。采用Legendre PRF的缘由主要有两点:其一,它在MPC的计算中非常高效;其二,其可确保托管比特具备更好的随机性。可参考这篇文章【5】获取更多细节,并且,我们将会在后续的文章中给出更加深入的解释。
MPC友好性
Eth 2.0 的设计目标之一是使其对MPC友好。其中包含了两个原因:其一,通过允许运营节点在多个计算机甚至不同的数据中心之间分布其验证人节点,从而避免单点故障,这可以带来额外的安全性;其二,通过一个无需信任(trustless)的验证人节点池,能够使资金较少的人可以参与Eth 2.0 验证。因此,托管证明也应该对MPC友好,这也是使用Legendre PRF的主要原因。由此,这或许会开启一种全新的业务模式,并产生许多其它有趣的应用。请参见此处【6】,获取更多细节。
PlatON发起了一个由以太坊基金会资助的项目,以实现和优化托管证明的MPC协议,当前代码已在GitHub【7】上开源。后续会公布更多细节,请持续保持关注!
注释
[1]Sharding FAQ · ethereum/wiki Wiki · GitHub
[2]Proof of Stake FAQ · ethereum/wiki Wiki · GitHub
[3]Data availability checks | Dankrad Feist
[4]https://github.com/ethereum/eth2.0-specs/blob/dev/specs/phase1/custody-game.md#misc
[5]Using the Legendre symbol as a PRF for the Proof of Custody - Sharding - Ethereum Research
[6]Carl Beekhuizen, Dankrad Feist · Ethereum 2.0 Trustless Staking Pools · SlidesLive
[7]GitHub - PlatONnetwork/proof_of_custody: MPC implementation of proof of custody
参考文献
(1)The Beacon Chain Ethereum 2.0 explainer you need to read first.
(2)Ethereum 2.0: A Complete Guide.
(3)Ethereum 2.0: A Complete Guide. Scaling, Part One.
(4)Ethereum 2.0: A Complete Guide. Scaling Ethereum —Part Two: Sharding.
This second installment will discuss sharding, the layer one scaling solution for Ethereum.
Reading time: 14 min read
(5)Proof of Stake FAQ.
(6)Data availability checks.
(7)A note on data availability and erasure coding.
(8)1-bit aggregation-friendly custody bonds.
TLDR: We present a 1-bit custody bond scheme which is friendly to BLS aggregation. Construction Let V be a 32-ETH collateralised validator that has published H(s) onchain where s is a 32-byte secret. Given a piece of data D the validator V can...
Reading time: 4 mins 🕑
Likes: 8 ❤
(9)Using the Legendre symbol as a PRF for the Proof of Custody.
TL;DR: Thanks to @JustinDrake’s construction in Bitwise XOR custody scheme, we can replace the “mix” function in the Proof of Custody scheme (currently SHA256) with any PRF that produces as little as only one bit of output. The Legendre PRF does...
Reading time: 6 mins 🕑
Likes: 6 ❤
(10)Proof of custody game design.
opened 08:19PM - 03 Feb 19 UTC
closed 10:57PM - 28 Mar 19 UTC
general:RFC
phase1
The basic proof of custody mechanism works as follows:
* For every (eg. 2 wee… k) period `p`, each validator calculates `rk[p] = BLS_sign(key=validator_privkey, msg=p)` as their round key.
* For every crosslink they participate in during that period, if that crosslink has data with chunks `D[0] ... D[size(D)-1]`, for each `D[i]` they compute `C[i] = mix(rk[p], D[i])` where `mix` is some function where for any `rk`, `mix(rk, x)` depends on `x`. They compute `R = custody_root(D)` as Merkle root of the `C[i]` values and sign `R mod 2` along with the crosslink (this is their "custody bit")
* During period `p + 1`, the validator must reveal `prevseed=rk[p]`, and the chain can verify that it is a correct value via `BLS_verify(key=validator.pubkey, msg=p, sig=prevseed)`
There are three types of byzantine behavior that we want to penalize:
1. Revealing `rk[p]` too early
2. Signing with some random custody bit because D is unavailable
3. Signing with the incorrect custody bit because even if D is available, the validator wishes to be malicious
For (1) we can have a special-purpose slashing condition; the only requirement is that _anyone_ must be able to trigger the condition and gain from doing so, so there should be a commit-reveal game to allow participants to trigger it without the block proposers being able to frontrun them.
(2) and (3) are similar cases, except (3) is more tractable. In case (3), once `rk[p]` is revealed, any third party can recompute `custody_root(D)`, check if the bit matches, and if the bit does not match start a challenge game, which they know ahead of time they will be able to win. First, they challenge to ask for the complete custody root, which must match the bit that has already been provided. At this point, the responder is free to respond with an arbitrary value of `R` that matches the same bit; for any `D`, it is almost always possible to find some data `D'` which differs from `D` in only one block where `custody_root(D') mod 2` is either 0 or 1. At this point, the responder has (and the challenger knows that the responder has) committed to some value which is _not_ equal to `custody_root(D)`.
The next step is for the challenger to ask for the two children of `R'` (we'll call them `C0` and `C1`). When the responder responds, the challenger can check which of the two don't match the corresponding values in the real custody Merkle tree for `D`. The challenger then asks for the two children of either `C0` or `C1`. This repeats `log(size(D))` times until eventually the responder must respond with some `C[i]` as well as a Merkle branch for the corresponding `D[i]`. The chain will check and find that the provided `C[i]` does _not_ match `mix(rk[p], D[i])`, and the responder can be penalized and the challenger can win. At this point, if the responder responds correctly, the challenger can be penalized.
Note that this whole process is only possible if all of `D` is available, so challengers can know whether or not they can successfully challenge. If `D` is not available, then we also need a challenge game which allows participants to ask for specific branches of `D` and demand an answer. Because data availability suffers from [fisherman's dilemma problems](https://github.com/ethereum/research/wiki/A-note-on-data-availability-and-erasure-coding), it's likely participants will not bother challenging unless challenging is free; hence, the proposed solution is to only allow block proposers to challenge, and give them a free allotment of challenges in each block, expecting them to fill the allotment.
Now, we have four types of challenges:
1. Input: attestation `A`, validator index `v`, data index `i`. Output: a Merkle branch of `D[i]` with the root matching `A.data_commitment`.
2. Input: attestation `A`, validator index `v`. Output: a root `R` matching `get_custody_bit(A, v)`
3. Input: attestation `A`, validator index `v`, index `i`, depth `d`, branch `B`, where `B` has as root the `R` value previously submitted by validator `v`. Output: the two children whose parent is the leaf in `B`.
4. Input: attestation `A`, validator index `v`, index `i`. Output: a Merkle branch of `D[i]` and `C[i]` with the roots matching `A.data_commitment` and the `R` value previously submitted by validator `v`.
Note that we can increase efficiency by merging (1), (2) and (4). We do this as follows:
* Input: attestation `A`, validator index `v`, data index `i`. Output: a Merkle branch of `D[i]` and `C[i]` with the roots matching, for the first branch, `A.data_commitment`, and for the second branch, the same `R` value as was submitted during any previous time the same validator answered a challenge for the same attestation.
We can also decrease the round count of the game, by asking for 2^k descendants some height k below the provided node (eg. 16 descendants 4 levels down). In this way, in the worst case (eg. a 2**24-sized data tree), the game would take only six rounds, instead of ~24.
#### How to implement the multi-round game
The main saving grace of all of the above is that the only game where honest challengers are not guaranteed to win (the branch challenge) only requires one round of challenging (all challenges can be done in parallel). Going beyond that, any honest challenger should be assured of victory, and hence willing to put down a deposit.
For each "exited" validator, we will maintain a counter, `challenge_round`, which starts at zero, and a bool `was_challenged_this_round`. When the validator reaches the end of their withdrawal queue, the following happens:
* If there were no challenges during this `challenge_round` of the validator (ie. `was_challenged_this_round = False`), or if `challenge_round = 6`, the validator withdraws successfully
* If there were challenges (any valid challenge sets `was_challenged_this_round` to `True`), the validator can skip back to the end of the exit queue as soon as they respond to all extant challenges, with `challenge_round += 1` and `was_challenged_this_round` reset to `False`.
* Challenging during round 0 is restricted to proposers. Challenging during round i+1 is restricted to anyone who challenged during round i.
Now, for economics (this is the part I am still less confident about). If a validator successfully answers all challenges, then every validator that challenged can be penalized some amount. If a responder does not answer challenges and the time hits some timeout period, then all validators that challenge get a reward out of the responder's deposit (these rewards could be evenly split, or only given to the first challenger of each challenge round, or split among the challengers of each round in a decreasing schedule, eg. the kth challenger of each round gets a reward of `(6/pi**2) / k**2` (the `6/pi**2` constant set so that rewards add up to a maximum of 1 per period).
(11)The proof of custody game.
(12)Ethereum 2.0 Trustless Staking Pools.